Errors in Hypothesis Testing

Outline

Type I error

Type II error

Power

Examples in the “real world”

Anytime we make a decision about the null it is based on a probability.  Recall that we reject the null when it tests a value that is unlikely for the known population.  Extreme values are unlikely for the population, but not impossible.  So, there is always some chance that our decision is in error.

Note that we will never know whether we know we have made an error or not with our hypothesis test.  When running a test, I only know what my decision is about the test, and not the true state of reality.  Thus, this discussion on errors is strictly theoretical.

Type I Errors

Whenever a value is less than 5% likely for the known population, we reject the null, and say the value comes from some other population, as shown in Figure 1.

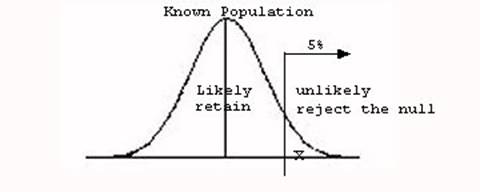
Figure 1

Notice that we are saying the value is really from another population distribution out there that we don’t know about as shown in Figure 2.

Figure 2

However, some of the time the value really does come from the known population.  Notice that even though the value represented is beyond the critical value it still lies under the curve for the normal population.  We reject any values in this range, even though they really are part of the known population.

When we reject the null, but the value really does come from the known population a Type I error has been committed.  A Type I error, then, happens when we reject the null when we really should have retained it.  Note that a Type I error can only occur when we reject the null.

The part of the distribution that remains under the curve for the known population but is beyond our critical value in the region of rejections is alpha (α).  When we set alpha we are setting the probability of making a Type I error as shown in Figure 3.

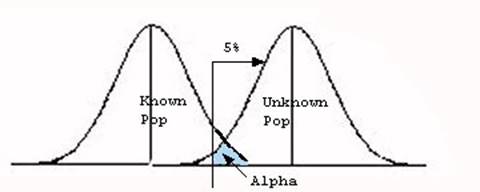
Figure 3

Type II Errors

Whenever a value is more than 5% likely for the known population, we retain the null, and say the value comes from the known population.  But, some of the time the value really does come from a different unknown population as shown in Figure 4.

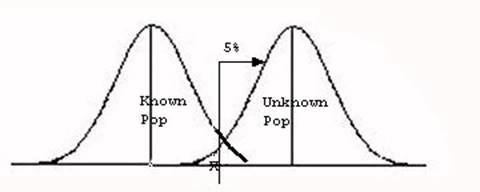
Figure 4

Notice in this situation the value is below the critical value, so we retain the null.  However, the value is still under the unknown population distribution, and may in fact come from the unknown population instead.  Thus, when I retain the null, when I should really have rejected it I commit a Type II error.

The probability of making a Type II error is equal to beta and not strictly defined by alpha.  Although we know the probability of a Type I error because we set alpha, a Type II error takes in a few more factors than that.  You can see the region of Beta (β) below.  Notice that it is the area below the critical value, but that is still part of the other unknown distribution as shown in Figure 5.

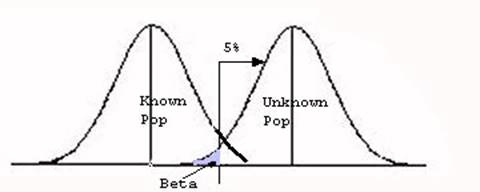
Figure 5

Power

Power is the probability of correctly rejecting the null hypothesis.  That is, it is the probability of rejecting the null when it is really false.  Again, we never really know if the null is false or not in reality.  Power is another way of talking about Type II errors.  Such errors have been recognized as a problem in the behavioral sciences, so it is important to be aware of such concepts.  However, we will not be computing power in this course.  You can ignore the “power” demonstration on the web page for that reason.

An easy way to remember all these concepts might be to put them in a table, much like your textbook does and shown in Table 1. 

Statistical Decision

Table 1

Reality	Reject Null	Retain Null
Null is True	Type I Error        (α)	Correct Decision        (1 – α)
Null is False	Correct Decision    (1 – β)	Type II Error      (β)

Examples of Errors in the “Real World”

Another way to think about Type I and Type II errors is to think of them in terms of false positives and false negatives.  A Type I error is a false positive, and a Type II error is a false negative.

A false positive is when a test is performed and shows an effect, when in fact there is none.  For example, if a doctor told you that you were pregnant, but you were not then it would be a false positive result.  The test shows a positive result (what you looking for is there), but the test if false.

A false negative is when a test is performed and shows no effect, when in fact there is an effect.  The opposite situation of the above example would apply.  A doctor tells you that you are not pregnant, when if fact you are pregnant.  The test shows a negative result (what you are looking for is not there), but the test is false.

Let’s look at another example.  A sober man fails a blood alcohol test.  What type of error has been committed (if any)? 

For this type of problem you will get two pieces of information.  First, whether the test was positive or negative.  The test is positive if what you are looking for is found.  It is negative if the test shows what you are looking for is not there.  The second piece of information is whether the test is in error or not (false or true test).  Thus, for this example, the test is positive because if you fail a blood alcohol test it is showing that there is alcohol in your system.  You are positive for alcohol in that case.  Since the man is sober, the test is false.  So, here we have a false positive test or Type I error.