Sampling Distributions
Sampling distributions represent a troublesome topic for many students. However, they are important because they are the basis for making statistical inferences about a population from a sample. A sampling distribution is a set of samples from which some statistic is calculated. The distribution formed from the statistic computed from each sample is the sampling distribution. If the statistic computed is the mean, for example, then the distribution of means from each sample form the sampling distribution of the mean. One problem sampling distributions solve is to provide a logical basis for using samples to make inferences about populations. Sampling distributions also provide a measure of variability among a set of sample means. This measure of variability will, in turn, allow one to estimate the likelihood of observing a particular sample mean collected in an experiment in order to test a hypothesis.
At the simplest level, when testing a hypothesis one is testing whether an obtained sample comes from a known population. If the sample value is likely for the known population then it is likely that the value must come from the known population. If the sample value is unlikely for the known population then it likely does not come from the known population, and it can then be inferred that it comes from a different unknown population instead. If some treatment is performed, like giving a drug to improve patient recovery time, then the average recovery time from a sample of the treated group will allow a test of the idea that the treatment had some effect (here on recovery time). Does giving patients this new drug in effect create a new and different population; a population using the drug? If the average recovery time of the treated group is very similar to, or likely for, the known population of patients that do not take the drug, then the treatment likely had no effect. If the average recovery rate is very different from, or very unlikely for, the known population of patients not taking the drug, then the treatment must have had an effect and created a new population of patients with different recovery times. Thus, some way to judge how likely a value is for the known population is needed.
The common formula used to find the probability or the likelihood of a value for a known population (solving z-score problems) is:
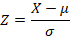
In the above formula the standard deviation, sigma (σ), gives information about how much variability exists in the population. Knowing how much variability exists in the population (the width of the distribution of scores) allows one to know how likely a single x-value is for that population. Because most values in a distribution will lie close to the mean, less likely values will fall farther from the mean. The wider the distribution of scores the less pronounced any specific difference between a value and the mean will be. For example, if the difference between an x-value and the population mean remains constant (in the numerator), then that difference will be much more likely if the population has a very wide distribution (large denominator) compared to its likelihood in a very narrow distribution (small denominator). So, any factor, like a decreased spread in the distribution of scores, that increases the relative difference between a value and the mean will lower our estimate of how likely the value is for the distribution.
However, when testing a hypothesis it is never based on a single x-value. Instead, a sample of values is used from which the average is computed. If the average or mean value tested is very different from the known population, then it can be assumed that the population the sample represents is not the same as the known population. The problem in using the above formula is that sigma gives information about how much individual values vary within a population, but nothing about how much sample means vary. Sampling distributions provide an explanation of how to measure variability in samples, and thus the probability of observing a particular sample mean.
Sampling Distribution of the Mean
Sampling distributions are theoretical, and not actually computed. However, examining the process of computing one is necessary. There are many types of sampling distributions, and a sampling distribution for any statistic can be formed. For the current discussion, the sampling distribution of the mean is most relevant. To form a sampling distribution:
1. Sample repeatedly and exhaustively from the population.
2. Calculate the statistic of interest (the mean) for each sample.
3. Form a distribution of the set of means obtained from the samples.
The values taken from the population to form a sample can be any specific size, but every possible sample of that size from the population must be taken. Then, an average of each sample is computed. The set of means obtained from each sample will form a new distribution, a sampling distribution. In this case, where the mean is computed as the statistic, it will be the sampling distribution of the mean. Every possible combination of values from the population is sampled to form a true sampling distribution. Since most populations are very large it is impractical to actually go through the process of forming a sampling distribution which is why they remain theoretical.
The first important fact learned from the sampling distribution of the mean is that the mean of the population and the mean of the sampling distribution of means will have exactly the same value. That is, the average of the entire population of single x-values is exactly the same as the average value obtained if each sample mean from the sampling distribution of means is averaged together. This fact is important to hypothesis testing because when testing a hypothesis based on a sample, even though a single sample will not likely yield a mean exactly the same as that of the population, on average it will be exactly the same. Thus, it is certain that repeated experiments will yield samples that will on average be the same as the population. Using a sample to make an inference about a population is therefore a logical and reasonable proposition.
The next important piece of information obtained from the sampling distribution of the mean is a measure of variability among sample means. Recall that some way to measure how much variability exists in a set of sample means is needed so that there will be some way to gauge how likely it is to obtain a particular sample mean collected in an experiment. If the mean value obtained in a sample is unlikely for the known population, then the population the value comes from is probably different from the known population. If the mean value obtained in the sample is likely or similar to the known population, then it is likely there is no difference between the population the value comes from and the known population. If there is a large amount of variability from sample to sample, an individual sample mean obtained to test a hypothesis will have to be much more different from the known population in order to stand out distinctively and to be considered unlikely for that population than if there is little variability from sample to sample. The standard deviation, just as with other distributions, will be the measure used to indicate the spread or dispersion of a distribution. Just as with the standard deviation of a population of individual values where the amount of variability that exists is measured by how much individual values deviate from the average, variability in the set of sample means will be computed the same way. When measuring the average deviation of a set of sample means in a sampling distribution, the amount of variability there is from sample to sample is being measured. This measure of the standard deviation of a distribution of sample means is called the Standard Error, and is symbolized as
Since the sampling distribution of the mean is theoretical, there is no need to actually calculate the standard error every time an inferential test is conducted. Instead, an estimate is made from the population or the sample. The formula to estimate the standard error from the population is:
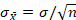
The above formula can be used if the population standard deviation is known. If so, it forms the denominator for a z-score hypothesis test:
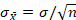
If the population standard deviation is not known, which is usually the case; the population standard deviation must be estimated from the obtained sample. Although the standard deviation estimated from a sample is calculated slightly differently than when all the population values are known, the computation of the standard error is essentially the same. In such cases the standard error is usually represented with Roman instead of Greek letters. So, the standard error is represented as and is computed with the formula:
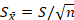
In addition, when using the sample to estimate the standard deviation we are no longer computing a z-test, but a t-test instead.
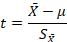
Notice that the denominator is an estimate of the standard error, and it is the same whether computing a z-test or a t-test. The distance a sample mean falls from the mean of the population is mediated by how much variability there is from sample to sample. If it is relatively unlikely to observe a certain sample (p < .05 for α = .05), then we can conclude that the sample did not come from the known population.
Finally, sampling distributions also yield information about how large a sample needs to be in order to test a hypothesis. The shape of the sampling distribution of the mean will always be normal regardless of the shape of the population distribution. Whether the population distribution has a normal, positively or negatively skewed, unimodal or bimodal shape, the sampling distribution of the mean will always have a “normal” (unimodal and symmetric) shape. That’s because when a distribution of sample means is formed, each value in the distribution is derived from a sample that contains a variety of scores from the population. Because each value in the sampling distribution is an average of these values from the population, most of the scores will lay close the mean of the population and create unimodal and symmetric distribution, even if the values in the population of single x-values do not.
Recall that when values are used to form a sampling distribution, samples of any size can be used. However, the larger the number of values in a sample taken from the population to form the sampling distribution, the more “normal” the sampling distribution will be. That’s because there will be a larger variety of values from the population in any individual sample, and the more likely the average from each sample will approximate the average value of the entire population. As it turns out, at around 30 values in a sample is when there is enough variety contained in the sample for those values to average out very close to the average of the population. However, the larger the number of values we take in a sample the closer we get to the average of the population. Since an estimate of the standard error is usually made from a sample, the sample size needs to be around 30 in order to approximate the value that would be obtained if the standard error was computed from the population. Thus, the minimum number of values needed to approximate the population with a sample is usually close to 30 and it is best to have this minimum number in any sample used for hypothesis testing.