Lesson 14
Independent Samples t-test
Outline
No Population Values
Changes in Hypotheses
Changes if Formula
-standard error
Pooled Standard Error
-weighted averages
Critical Values
-df
Sample Problem
No Population Values
With the independent samples t-test we finally reach the point where we have no population values. This fact is important because when we test hypotheses we are usually testing an idea and a population that we know nothing about. Think about the kinds of scientific discoveries you hear about often. New treatments for diseases, new drugs, or new techniques for improving depression all involve testing a population created by the treatment or drug or technique.
So, with the independent samples t-test we will compare two sample values directly. Note that we are still making the inference about the populations from which the samples are drawn.
Changes in Hypotheses
All hypotheses from this point on in the course will be two-tailed. In addition, since we no longer no any population values we will use “mu” to represent both populations.
So for example, H0: μdiet = μplacebo
H1: μdiet ≠ μplacebo
Formula Changes
Recall the formula for the t-test we have been using: , where
The numerator will now have two sample values instead of one sample and one population. The denominator, recall, is the standard error (the standard deviation divided by the square root of the sample size).
Our standard error (denominator) was: Remember that the standard error measures variability we expect to see among samples. Now that we have two samples we will want to include the estimate of variability from both. Thus, we will have to take into account the standard deviations and sample sizes of both samples. We will compute the standard error separately for each sample and then add them together.
Because of the formula we will develop, it will be easier if we switch from using the standard deviation to the variance. In this way we can eliminate the radical in the denominator. The two formulas are equivalent:
=
Notice that we now denote the combined standard error with (). Again, it’s just a way to symbolize the final value we will divide into the numerator.
where
Critical Values
We will use the same table to find the critical values as we did with the one-sample t-test. However degrees of freedom are now computed from two samples, so: df = n1 + n2 – 2
Sample Problem
A new program of imagery training is used to improve the performance of basketball players shooting free-throw shots. The first group did an hour imagery practice, and then shot 30 free throw basket shots with the number of shots made recorded. A second group received no special practice, and also shot 30 free throw basket shots. The data are below in Table 1. Did the imagery training make a difference? Set alpha = .05.
Table 1
| X1 | X2 |
| 15 | 5 |
| 17 | 6 |
| 20 | 10 |
| 25 | 15 |
| 26 | 18 |
| 27 | 20 |

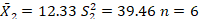
H1: The population receiving imagery practice will make a different number of baskets than the population receiving no imagery practice.
Step 1: Write the hypotheses in words and symbols
H0: The population receiving imagery practice will make a different number of baskets than the population receiving no imagery practice.
H1: μimagery. ≠ μno imagery
H0: μimagery = μno imagery
Step 2: Find the critical value for the test
Since alpha is .05, and it is a two-tail:
tcritical = ±2.228
Step 3: Run the test
Since we have equal sample sizes (n’s) for each group we can use the first (shorter) formula:
where
All the values are given above, so you just have to plug and compute.
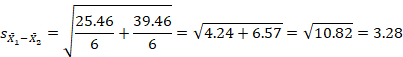
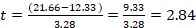
Step 4: Make a decision about the Null
Reject the Null. Since the value we computed in Step 3 is more extreme than the critical value in Step 2, we reject the idea that they are from the same population.
Step 5: Write a conclusion
The population of players with imagery training made a different number of baskets compared to those with no training.