Lesson 18
Regression
Outline
Equation of a Line
-Slope
-Y-Intercept
-regression line
Making Predictions
Error in Prediction
-residual variation
-standard error of the estimate
Regression is very similar to correlation, but instead of measuring the relationship we will make predictions based on the relationship. Even though we are not inferring a causal relationship, we can nevertheless predict one variable if we have information about the other. We will refer to X as the predictor variable, and Y as the criterion variable. Thus, we will attempt to use X in order to predict what Y should be.
Equation of a Line
Recall that when we were first looking at scatter plots and we drew a line through the dots in order to indicate the direction of the effect. With regression, that is exactly what we want to do. We will compute the best fitting line for the data that we have. In a scatter plot a single line will not hit every data point, but we will construct a line that simultaneously comes as close to each data point as possible.
As with similar topics in geometry, we will express the line we come up with in an equation. You may recognize Y = mx + b. We will use a similar equation to express a straight line, though our Y-value will not be the same value we have in our data, but instead be the value we would predict for Y. Since our data are scattered about, it is unlikely that the value our line would predict for Y is actually a point in our data set. Thus, our equation for the line will be slightly different:
ßEven though we use “b” here, it is still the slope of the line, and “a” is the y-intercept. We also use
instead of just Y to indicate that this is a predicted value for way based on the regression line rather then an actual Y-value.
In order to make predictions, we will compute these regression coefficients (b and a), and plug them into our equation. We can then plug in an X-value and get out a predicted Y value ().
Slope
Slope is the unit change in Y for each single unit change in X. That is, since we will multiply the slope with the X-value we want to make predictions about, the predicted Y will change by the amount of the slope for each single unit of X.
Slope computation is very similar to correlation. In fact, if you have already computed the correlation you can use the same values to compute slope.
<–Notice that we have the covariation of X and Y in the numerator, so the entire numerator will be the same as with r. The denominator is the sums of squares for X. This was a portion of the denominator for r as well.
Y-Intercept
The y-intercept is the point at which the regression line crosses the Y-axis. It is also the value we predict for Y when X = 0. That’s because we are at the Y-axis when X=0.
<–Notice that we must compute the slope “b” before we can compute the y-intercept.
Making Predictions
Once we have computed the regression coefficients, we can put them into our equation for a line and start making predictions. Let’s look at an example problem. For this problem we will continue with the example we used with correlation (see Table 1).
Table 1
| # Years of College (X) | Income (Y) | X2 | Y2 | ΣXY |
| 0 | 15 | 0 | 225 | 0 |
| 1 | 15 | 1 | 225 | 15 |
| 3 | 20 | 9 | 400 | 60 |
| 4 | 25 | 16 | 625 | 100 |
| 4 | 30 | 16 | 900 | 120 |
| 6 | 35 | 36 | 1225 | 210 |
| | | |
Now, however, we will compute the equation of the line that predicts income from number of years in college. First compute slope and y-intercept.
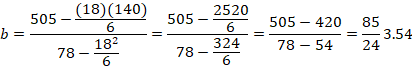
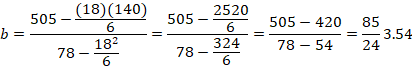
Once these values are computed, we can write the equation of the line.
=3.54X + 12.7
Now we simply plug in an x-value that would like to make a prediction about. Note again that this equation will not yield an actual y-value, but a prediction on the line that best describes the relationship between X and Y.
For example, what income would we predict for someone with five years of education?
=3.54(5) + 12.7
=17.7 + 12.7
=30.4
Here we just insert the X-value, and compute Y. So, we expect someone with five years of education to make about 30 thousand dollars a year.
Error in Predictions
The amount our predicted Y-value differs from the actual Y-value in our data is error or residual variation. If we average this residual variation for all of our scores, we can get a measure of the error our equation yields. The standard error () is the average deviation between actual Y and predicted Y.
If we first plug in each X-value from our data into the regression line to get out a predicted Y-value, then we can see how different the Y and predicted Y-values differ (see Table 2).
Table 2
| # Years of College (X) | Income (Y) | Ŷ |
| 0 | 15 | 12.7 |
| 1 | 15 | 16.24 |
| 3 | 20 | 23.32 |
| 4 | 25 | 26.86 |
| 4 | 30 | 26.86 |
| 6 | 35 | 33.94 |
=3.54X + 12.7
Remember the residual variation is the difference between Y and Ŷ. Once we find this difference we want to add the differences to get an average (see Table 3).
Table 3
| # Years of College (X) | Income (Y) | Ŷ | Y- Ŷ |
| 0 | 15 | 12.7 | 2.3 |
| 1 | 15 | 16.24 | -1.24 |
| 3 | 20 | 23.32 | -3.32 |
| 4 | 25 | 26.86 | -1.86 |
| 4 | 30 | 26.86 | 3.14 |
| 6 | 35 | 33.94 | 1.06 |
Notice that we have the same problem here as with standard deviation. The sum of the deviations about the mean must always equal zero. In fact, the standard error of the estimate we are calculating is the standard deviation of the regression line we computed. So, we will square the difference score we computed in the last step so that we can add the squared differences. The formula we are working toward looks like this:
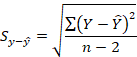
So, all we have left to do is square our residual variations, sum them, divide by df, and take the square root of the whole thing (see Table 4).
Table 4
| # Years of College (X) | Income (Y) | Ŷ | Y- Ŷ | (Y- Ŷ)2 |
| 0 | 15 | 12.7 | 2.3 | 5.29 |
| 1 | 15 | 16.24 | -1.24 | 1.54 |
| 3 | 20 | 23.32 | -3.32 | 11.02 |
| 4 | 25 | 26.86 | -1.86 | 3.46 |
| 4 | 30 | 26.86 | 3.14 | 9.86 |
| 6 | 35 | 33.94 | 1.06 | 1.12 |
Plugging into the formula we have:
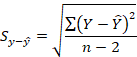
Our interpretation is that on average actual Y and predicted Y differ by 2.85 units. So, any prediction we make about income using the equation will be off by about $2,850.