Lesson 19
Chi-Square
Outline
Categorical Data
Goodness of Fit Test
-observed frequency
-expected frequency
-X2 statistic
Example
-hypothesis testing
Categorical Data
As mentioned at the start of the lesson with correlation, all of the data we have been working with so far involve measurement data. We actually took measurements from units in our sample to create our distribution. Often times, however, we will want to analyze categorical or qualitative data as well. For categorical data we will not have a measure of individual units in the sample. Instead, we will analyze frequencies or counts of people falling into different categories or groups. When analyzing categorical data we say the test is non-parametric. Thus, all the tests we have learned before this point were parametric tests.
Chi-Square Goodness-of-Fit Test
We will learn two different Chi-square tests. The first of these is the goodness-of-fit test. With the goodness-of-fit test we will test whether the data “fit good” with what we would expect if only chance factors were operating. For example, if I measured the number of insurance claims for different car types, I might have the data in Table 1.
Table 1
| High Performance | Compact | Mid-Size | Full Size |
| 20 | 14 | 7 | 9 |
Notice that our data is now frequency values or how many values in our sample fit into different categories. The test will tell us whether there is a difference in how many values fall at different levels of the single variable (car type). Is there a difference in number of claims for different car types?
The values we observe in our sample are the observed frequencies (). What we want to know is if they differ from the frequencies we would observe by chance. The values we would expect if there really was no difference in the number of claims made for different car types are what we call the expected frequencies (
). If there really was no difference in the frequencies for each level of the variable, then we would expect equal numbers of claims for each car type. Since there a total of 50 claims in our sample, and there are 4 different levels of the variable, then we would expect 12.5 claims for each car type (see Table 2).
Table 2
| High Performance | Compact | Mid-Size | Full Size | |
| 20 | 14 | 7 | 9 | Observed |
| 12.5 | 12.5 | 12.5 | 12.5 | Expected |
What the Chi-square statistic does is to compare the values we observe to those we would expect if there was no difference. If what we observe varies a good bit from the values we would expect if there was not difference, then there must be a difference. If there really was no difference in the number of insurance claims, for this example, then we would expect the number of claims to be close to the expected frequencies.
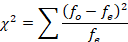
Notice that we subtract each expected value from each observed value, square the difference, and divide by the expected frequency. We then sum up all of the values we computed.
Let’s take a look at the example we have been working on within the context of hypothesis testing. We will continue the problem with Alpha set to .05.
Step 1: Write the Hypotheses for the test.
H1: f0 ≠ fe
H0: f0 = fe
Here we are stating that the observed frequencies are the same as the expected for the null.
Step 2: Find the Critical Value
Again we will use Appendix A to find the critical value, see page A-34. For our test degrees of freedom is equal to C – 1, where C is the number of categories
Df = 4 – 1 = 3
X(critical)= 7.81
Step 3: Run the Statistical Test
We have already computed the expected values (see Table 3), so we just need to plug the numbers into the formula.
Table 3
| High Performance | Compact | Mid-Size | Full Size | |
| 20 | 14 | 7 | 9 | Observed |
| 12.5 | 12.5 | 12.5 | 12.5 | Expected |
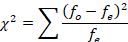
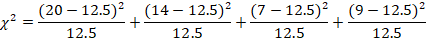

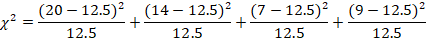
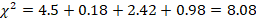
Step 4: Make a Decision About the Null
Reject the null. The value we computed in Step 3 is larger than Step 2, so we reject the null.
Step 5: Conclusion
Since we rejected the null we say there is a difference in the number of claims made for different car types.