Lesson 20

Chi-Square (Test of Independence)

Outline

Measuring Independence

-observed frequencies

-expected frequencies

-chi-square

Measuring Independence

The Chi-square test of independence is similar to the test we just learned in the last lesson.  However, instead of measuring frequencies along only one dimension, we will measure frequencies for two variables at the same time.  Our test is designed to test whether or not these two variables are independent (not related).  If we reject the null and say the variables are not independent of one another, then we have established that the two variables are related. 

The test of independence starts with frequencies or counts we observe in our sample, or the observed frequencies.  For this example in Table 1, a sample of 50 people is used to record personality and color preference is measured:

Table 1

	Blue	Red	Yellow
Extroverted	5	20	5
Introverted	10	5	5

                                                Observed Frequencies

Is there a relationship between personality type and color preference?  Our hypotheses will state exactly that, with the null as usual stating that there is no effect or no relationship.

H₁:  There is a relationship between color preference and personality type (variables are not independent).

H₀:  There is no relationship between color preference and personality type (variables are independent).

Since we have two variables, our degrees of freedom will change. 

df = (R – 1) (C- 1) ß where R is the number of rows and C is the number of columns in our table.  There are two rows going across and three rows going down.  So, degrees of freedom for this example are:

df = (2 – 1) (3- 1) = (1)(2) = 2

We will find the critical value using the same table we used in the goodness-of-fit test.  In our example:

χ² = 5.99

When we start to compute the statistic, it will be similar to the goodness-of-fit test as well.  However, we will need a formula to compute the expected frequencies instead of just dividing our sample size equally between groups. We will need to compute the expected value separately for each observed value in our sample.  So, in our example we must compute six different expected frequencies.  Note that our expected frequencies with this test are the values we expect if the null is true.  Thus, the expected frequencies are the values we expect if there is no relationship or the variables are independent.

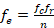
The value n is the total or 50 here.  In the numerator we have the frequencies for the “c” column and “r” row.  You multiply these values together.  They are the total frequency for the row and column of the individual expected value we are looking for with the computation.  So, you must first add up the frequencies for each row and column as seen in Table 2.

Table 2

	Blue	Red	Yellow	Total
Extroverted	5	20	5	30
Introverted	10	5	5	20
Total	15	25	10

Each value of our six observed values will have separate column frequency () and row frequency ().  For example the observed value in the first row and column (5) has a row frequency of 30 and a column frequency of 15.

Continue finding each expected frequency in this same way for each of the observed values.  Notice that when we compute a different expected frequency our row and column frequencies will change.  So, for the next value (extroverted and red):

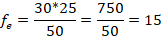
Again, you continue the process until you have found all the expected frequencies.  There is a shortcut for finding the rest of these values if you feel comfortable with the statistic.  Once we compute these two expected frequencies all the others are determined (hence the two degrees of freedom).  All of our expected frequencies must have the same row and column sums as our observed frequencies.  So, once we have computed these two expected frequencies all of the other values can be found by subtracting out the row or column total.  The remaining unknown expected value in the first column, then, must be the number that will make that first column add up to 15.  Since the first expected value is 9, then the remaining number must be 15 – 9 = 6. 

Whether you compute each individual expected frequency or use the short cut, you will get a complete table of expected frequencies, as seen in Table 3.

Table 3

	Blue	Red	Yellow
Extroverted	9	15	6
Introverted	6	10	4

                                                Expected Frequencies

The process for finding the final Chi-square value is the same as before.  We will find the difference between our expected and observed frequencies, square the difference, and then divide by the expected frequency for each value in our table.

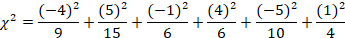
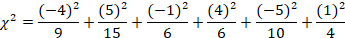
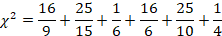
 = 1.78+1.67+0.167+2.67+2.5+.25

 = 9.04

Since this value is greater than our critical value, we will reject the null here and say there is a relationship.  Thus, knowing someone’s personality type gives you information about their likely color preference.